Formulas
An equation is a mathematical statement indicating that two expressions are equal. The expressions can be numerical or algebraic. The equation is not inherently true or false, but only a proposition. The values that make the equation true, the solutions, are found using the properties of real numbers and other results. For example, the equation has the unique solution because when we substitute 3 for in the equation, we obtain the true statement . A formula is an equation expressing a relationship between constant and variable quantities. Very often, the equation is a means of finding the value of one quantity (often a single variable) in terms of another or other quantities. One of the most common examples is the formula for finding the area of a circle in terms of the radius of the circle: . For any value of , the area can be found by evaluating the expression .Example 11: Using a Formula
A right circular cylinder with radius and height has the surface area (in square units) given by the formula . Find the surface area of a cylinder with radius 6 in. and height 9 in. Leave the answer in terms of .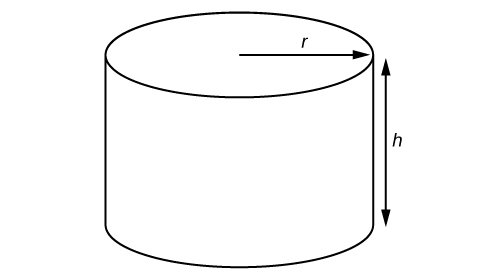 Figure 3. Right circular cylinder
Figure 3. Right circular cylinderSolution
Evaluate the expression for and .\begin{array}\text{ }S\hfill&=2\pi r\left(r+h\right) \\ \hfill& =2\pi\left(6\right)[\left(6\right)+\left(9\right)] \\ \hfill& =2\pi\left(6\right)\left(15\right) \\ \hfill& =180\pi\end{array}
The surface area is square inches.
Try It 11
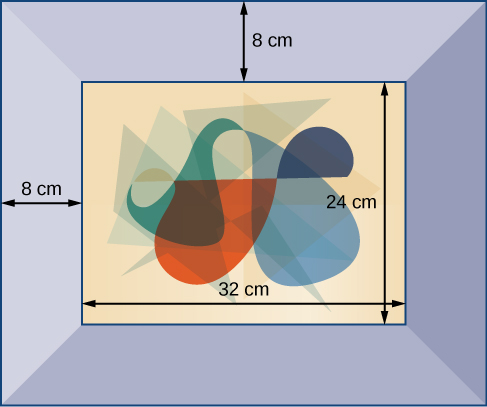 Figure 4
Figure 4