Solutions
Solutions to Try Its
1. y-intercept ; x-intercepts , and 2. The graph has a zero of –5 with multiplicity 1, a zero of –1 with multiplicity 2, and a zero of 3 with even multiplicity. 3. 4. Because f is a polynomial function and since is negative and is positive, there is at least one real zero between and .
5.
6. The minimum occurs at approximately the point , and the maximum occurs at approximately the point .
4. Because f is a polynomial function and since is negative and is positive, there is at least one real zero between and .
5.
6. The minimum occurs at approximately the point , and the maximum occurs at approximately the point .
Solutions to Odd-Numbered Exercises
1. The x-intercept is where the graph of the function crosses the x-axis, and the zero of the function is the input value for which . 3. If we evaluate the function at a and at b and the sign of the function value changes, then we know a zero exists between a and b. 5. There will be a factor raised to an even power. 7. 9. 11. 13. 15. 17. 19. 21. 23. 25. and . Sign change confirms. 27. and . Sign change confirms. 29. and . Sign change confirms. 31. 0 with multiplicity 2, with multiplicity 5, 4 with multiplicity 2 33. 0 with multiplicity 2, –2 with multiplicity 2 35. 37. 39. with multiplicity 2, 0 with multiplicity 3 41. 43. x-intercepts, with multiplicity 2, with multiplicity 1, y-intercept . As , , as , . 45. x-intercepts with multiplicity 3, with multiplicity 2, y-intercept . As , , as , .
45. x-intercepts with multiplicity 3, with multiplicity 2, y-intercept . As , , as , .
 47. x-intercepts with multiplicity 1, y-intercept . As , , as , .
47. x-intercepts with multiplicity 1, y-intercept . As , , as , .
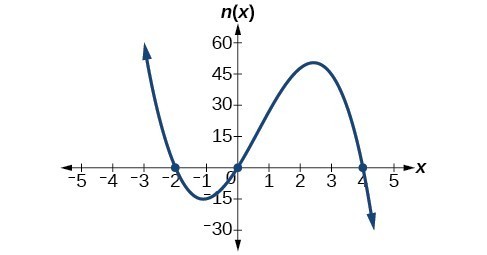 49.
51.
53. –4, –2, 1, 3 with multiplicity 1
55. –2, 3 each with multiplicity 2
57.
59.
61.
63.
65.
67. local max , local min
69. global min
71. global min
73.
75.
77.
79.
49.
51.
53. –4, –2, 1, 3 with multiplicity 1
55. –2, 3 each with multiplicity 2
57.
59.
61.
63.
65.
67. local max , local min
69. global min
71. global min
73.
75.
77.
79. 